通信原理期末复习

第一章绪论

1. 基本概念

1.1 消息、信息和信号

消息: 对事物的物理状态变化的描述　(如：温度、语音、文字、图像)
信息: 消息中有用的内容
信号: 为传递消息使用的方式

1.2 通信

由一地向另一地传递消息(信息)

1.3 通信模型

@startuml
(*)-right-> "信源" 
-right->[发送端] "发送设备"
-right-> "信道" as A1
-right-> "接收设备"
-right->[接收端] "信宿" as A2
"噪声源 "-up-> A1
A2 -right-> (*)
@enduml

信源: 消息的产生地
发送设备: 将原始电信号转换为适于在信道中传输的信号(变换、编码、调制)
信道: 传输媒介或途径
噪声源: 散布在系统各部分的噪声集中表现，噪声降低通信质量
接受设备: 将信号转换为原始信号(调解、译码)
信宿: 信息的归宿点，将电信号转换为相应消息

2. 信息的度量

1. 信息量

$信息量: I = log_a{\frac{1}{P(x)}} = -log_a{P(x)}$

一般以2为底 $I = log_2{\frac{1}{P(x)}}$ 单位为 bit(比特)
以e为底单位是奈特

2. 平均信息量

由M个符号组成的消息, 每个符号所含的平均信息量为:

$H(X) = - \sum_{i=1}^M{P(x)log_2{P(x_i)}} \space (bit/符号)$

最大熵条件为各符号独立等概

$H(X) = log_2M$

3. 性能指标

3.1 可靠性和有效性

数字通讯
1. 有效性: 传输速率
2. 可靠性: 误码率
模拟通讯
1. 有效性: 有效传输频带(有效带宽)
2. 可靠性: 传输信噪比

3.2 数字通讯传输速率、频带利用率

码元传输速率:

$R_s=\frac{1}{T_s}(Baud)$
1. 单位波特(Baud)
2. $R_s$ : 码元传输速率
3. $T_s$ : 码间间隔
信息传输速率(传信率)
1. 单位: 比特/秒、bit/s 、b/s　、bps
2. 对于M进制,的等概率数字系统 $R_b=R_s \times log_2M (bit/s)$
3. 若出现的概率不同 $R_b=R_s \times H(X) (bit/s)$
频带利用率 $\eta$
1. 传输速率(R)和频带宽度(B)之比,即单位频带内的传播速率
  - $\eta = \frac{R_s}{B} 或 \eta = \frac{R_b}{B} $
  - B 为所需带宽

3.3 差错率

误码率
- $P_e = \frac{错误接受的码元数}{传输总的码元数}$
误信率
- $P_b = \frac{错误接受的比特数}{接受的总比特数}$
关系
- 对于二进制 $P_e = P_b$
- 对于M进制 $P_e \geq P_b$

第二章信道

1. 分类

狭义信道: 传输信号的媒介
广义信道: 扩大了范围的信道

@startmindmap
* **信道**
** 狭义信道
***[#Orange] 有线信道: 明线、对称电缆、同轴电缆、光
***[#Orange] 无线信道: 短波电离层反射、对流层散射
** 广义信道
***[#Orange] 调制信道
****[#bfa] 恒参信道: 明线、对称电缆、同轴电缆、光纤
****[#bfa] 随参信道:  短波电离层反射、对流层散射
***[#Orange] 编码信道
****[#bfa] 有记忆信道
****[#bfa] 无记忆信道
@endmindmap

2. 信道模型

2.1 调制信道模型

二对端信道模型
- $e_0{t}=f{e_i(t)}+n(t)$
$f(e(t))$ $f (e (t))$ 为信道对信号影响的某种函数关系,可设想成与干扰相乘的形式,因此可写成下面式子
- $e_0(t) = k(t) \cdot e_i{t}+n(t)$
- 恒参信道: $k(t)$ 不随时间变化，或变化很慢
- 随参信道: $k(t)$ 随时间变化

3. 恒参信道

3.1恒参信道一般特性

幅度－频率特性(简称幅频特性) 和相位－频率特性(简称相频特性)
- $H(\omega) = |H(\omega)|e^{j\phi(\omega)}$
- $|H(\omega)|$ 为幅频特性
- $\phi(\omega)$ 为相频特性
恒参信道对信号传输的影响是:
1. 对信号在幅度上产生固定的衰减
2. 对信号在时间上产生了固定的迟延J
- 以上两条满足了信号无失真传输的条件

4. 随参信道

特点
1. 信号衰耗随时间随机变化
2. 信号传输的时延随时间随机变化
3. 多径传播

5. 连续信道容量

信道容量公式(香农公式)
- $C = Blog_2{1+\frac{S}{N}} \space (bit/s)$
- B(Hz) 为带宽
- S(W) 为功率
- N(W) 为加性高斯噪声
信噪比: $dB = 10 \times log_{10}(S/N)$
结论
1. 增大功率、减少噪声都可以增加,都可以让信道容量趋于无穷大
2. 增大信道带宽不能让信道不能让信道容量趋于无穷大

第三章模拟调制系统

1. 模拟调制的概念

模拟调制的功能
1. 适合信道传输
2. 实现有效辐射
3. 实现频率分配
4. 实现多路复用
5. 提高系统抗噪声性能
分类
1. 按调制信号 $(m(t))$ 不同: 模拟调制和数字调制
2. 按载波 $(c(t))$ 不同: 连续波调制、脉冲波调制
3. 按所调载波的参数不同
  - 幅度调制
  - 频率调制
  - 相位调制
4. 调制器 $H(\omega)$ $H (ω)$
  - 线性调制: 振幅(AM)、双边带(DSB)、单边带(SSB)、残留边带(VSB)
  - 非线性调制: FM，PM

2. 振幅调制(AM)

2.1 AM时域表达式

$S_{AM} = [A_0+m(t)]\cos\omega_ct$
$A_0$ 为外加直流分量
$m(t)$ 为输入调制信号,无直流分量,最高频为 $f_m$ (原始信号)
$\omega_c$ 为载波的频率,必须有 $|m(t)|_{max} \leq A_0$

2.2 AM频域表达式

结论
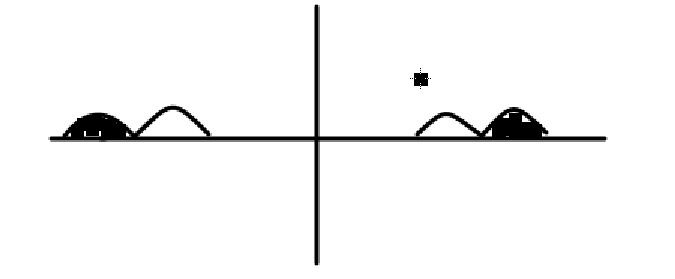
1. 调制后频谱形状没有变化，仅仅是信号频谱位置发生了变化
2. AM信号由 $\pm\omega_c$ 处的冲激函数和 $\pm\omega_c$ 两边的边带频谱组成
3. 调制前基带信号的频带宽度为 $f_m$ , 调制之后为 $2f_m$
边带: 阴影部分为上边带(USB), 其余为下边带(LSB)

2.3 平均功率

$P_{AM} = \frac{A_0}{2}+\frac{\overline{m^2(t)}}{2} = P_c + P_s$
其中:
- $P_c =\frac{A_0}{2}$ 为载波功率
- $P_s =\frac{\overline{m^2(t)}}{2}$ 为边带功率
- 只有边带功率与信号有关，载波分量不携带信息

2.4 AM信号调制效率

通常把边带功率 $P_s$ 与信号总功率 $P_AM$ 的比值称为调制效率,用符号 $\eta_{AM}$ 表示

$\eta_{AM} = \frac{P_s}{P_{AM}} = \frac{\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}$

2.5 AM解调

相干解调
非相干解调

3. 抑制载波双边带(DSB)

3.1 DSB 的时域表达式

$S_{DSB} = m(t)\cos(\omega_ct)$

3.2 DSB平均功率:

$P_{DSB}=\frac{1}{2}\overline{m^2(t)}=P_s$

3.3 DSB调制效率:

$\eta_{DSB} = \frac{P_s}{P_{DSB}}=100\%$

3.4 DSB解调

只能相干解调

3.5 频带宽度

$B_{DSB}=2f_m$

3.6 其他

公式: $2\cos\alpha\cos\beta =\cos(\alpha-\beta)+\cos(\alpha+\beta)$
USB 上边带: $\cos(\alpha+\beta)$
LSB 下边带: $\cos(\alpha-\beta)$

4. 单边带调制(SSB)

4.1 SSB 的时域表达式

$S_{SSB}(t) = \frac{A}{2}\cos(\omega_c \pm \omega_m)t$

4.2 频带宽度

$B_{DSB}=2f_m$

4.3 平均功率

$P_{SSB} = \frac{1}{2} P_{DSB} = \frac{1}{4} \overline{m^2(t)}$

5. 残留边带(VSB)

发送功率和频带宽度(都介于单边带和双边带之间)
- $P_{SSB} \leq P_{VSB} \leq P_{DSB}$
- $B_{SSB} \leq B_{VSB} \leq B_{DSB}$

6. 线性调制系统抗噪声性能

输出信噪比,定义:
$\frac{s_i}{n_i}=\frac{解调器输入已调信号平均功率}{解调器输入噪声平均功率}=\frac{\overline{s_m^2(t)}}{\overline{n_i^2(t)}}$

6.1 DSB 调制系统性能

输入信噪比
- $\frac{S_i}{N_i}= \frac{\overline{m^2(t)}}{2N_0B_{DSB}}$
输出信噪比
- $\frac{S_0}{N_0}= \frac{\overline{m^2(t)}}{N_0B_{DSB}}$
制度增益
- $G_{DSB} =\frac{S_0 / N_0}{S_i / N_i} = 2$

6.2 AM 调制系统性能

输入信噪比
- $\frac{S_i}{N_i}= \frac{A_0^2\overline{m^2(t)}}{2N_0B_{DSB}}$
输出信噪比
- $\frac{S_0}{N_0}= \frac{\overline{m^2(t)}}{N_0B_{DSB}}$
制度增益
- $G_{DSB} =\frac{S_0 / N_0}{S_i / N_i} =\frac{2\overline{m^2(t)}}{A_0^2+m^2(t)} = 2$
- $G_AM$ 最大为 $\frac{2}{3}$

6.3 SSB 调制系统性能

输入信噪比
- $\frac{S_0}{N_0}= \frac{\overline{m^2(t)}}{4N_0B_{DSB}}$
输出信噪比
- $\frac{S_0}{N_0}= \frac{\overline{m^2(t)}}{4N_0B_{DSB}}$
调制制度增益
- $G_{DSB} =\frac{S_0 / N_0}{S_i / N_i} = 1$

第四章模拟信号数字化传输

1. 采样定理(抽样定理):

1.1 低通抽样定理

频带限制在 $(0,f_H)$ 内的时间连续信号 $m(t)$ , 如果抽样频率 $f_s$ 大于或等于 $2f_H$ ,则可以由抽样值序列 $m_s(t)$ 无失真重建 $m(t)$
奈奎间隔: 最大允许抽样间隔 $T \leq \frac{1}{2f_H}$
奈奎斯特速率: 最低抽样速率 $f_s = 2f_H$

1.2 带通抽样定理

一个带通信号m(t), 其频率限制在 $f_L$ 与 $f_H$ 之间,带宽 $B=f_H-f_L$ ,则最小抽样速率 $f_s=\frac{2f_H}{m}$ 其中m是一个不超过 $\frac{f_H}{B}$ 的最大整数
若最高频率 $f_H$ 为带宽的整数倍,即 $f_H=nB$ ,最小抽样频率为 $f_s= 2B$
若最高频率 $f_H$ $f_{H}$ 不为带宽的整数倍,即
- 因为 $f_H= nB + kB, \space n<k<1$ , m 为小于(1+k)的最大整数， m =n
- 最小抽样速率: $f_s = 2B(1+ \frac{k}{n})$

2. 脉冲振幅调制(PAM)

用周期窄的脉冲信号近似代替冲击脉冲信号
- 自然抽样
- 平顶抽样

3. 量化

3.1 均匀量化

若输入信号最大最小值分别为a,b,量化电平数为M,那么量化间隔为:
- $\Delta_i = \Delta=\frac{b-a}{a}$

3.2 非均匀量化

A 压缩率

$y= \begin{cases} \frac{Ax}{1+lnA} & 0 \leq x \leq \frac{1}{A} \\\\\\ \frac{1+lnAx}{1+lnA} & \frac{1}{A} \leq x \leq 1 \end{cases}$

$\mu$ 压缩率

$y=\frac{ln(1+\mu x)}{ln(1+\mu)}, \space 0 \leq x \leq 1$

13 折线
- 13折线非常逼近A=87.6 的对数压缩特性
15 折线
- 逼近 $\mu$ 率压缩( $\mu = 255$ )